Neural Collaborative Filtering - Xiangan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, Tat-Seng Chua (2017)

Abstract
nerual network 기반의 collaborative filtering을 개발함.
MF는 user와 item 공간의 latent vector들의 inner product를 통해 두 관계를 표현함. inner product NCF를 제시함으로써, 보다 유연한 방식으로 두 관계를 표현할 수 있는 일반화된 프레임워크를 제시함.
DNN을 사용하여 data로부터 interaction function을 배움.
y_u,i=1 user u와 item i 간의 상호작용이 있음.
y_u,i=0 상호작용이 없음, 해당 item을 모를 경우에도 0이 됨.
- 상호작용 : user가 item을 열람했거나, 구매했거나 등의 implicit feedback, explicit preference를 뜻하는 것이 아님.
⇒ 추천 문제 : y_u,i가 1이 될 확률을 예측하는 문제로 귀결됨.
Framework
MF : user-item 행렬을 저차원의 행렬 2개로 분해
pu와 qi의 내적으로 추정함. → linear 모델은 user와 item 간의 복잡한 관계를 표현하는 데 한계가 있음.
NCF : Neural Collaborative Filtering

input Layer (sparse) : user-item 사이의 one-hot encoding 벡터
Embedding layer : sparse 벡터를 dense하게 바꿔주는 역할
input단계의 sparse 벡터를 dense 벡터로 맵핑.
dense 벡터를 얻기 위해 임의로 가중치를 초기화하지만 별도의 fcnn을 사용할 수도 있음.
가중치 행렬 P를 얻게 됨 : P는 m차원의 sparse 벡터를 k 차원의 공간에 정사영하는 변환행렬으로 볼 수 있음.
각 행은 유저를 표현하는 저차원의 dense 벡터가 되고 이를 user latent vector로 사용하게 됨.
마찬가지로 가중치 행렬 Q는 k차원의 공간에 정사영하는 변환행렬로 이를 item latent vector로 사용하게 됨.
Neural CF Layer
user latent vector와 item latent vector를 합친 벡터를 input으로 받아 dnn 층을 통과함.
Output Layer
yu,i의 추정치를 구하는 단계로 user u와 item i가 얼마나 관련 있는지를 나타내며 0과 1 사이의 값을 가짐. logistic, probit 함수를 사용함.
NCF layer의 hidden vector를 input으로 받아 yu,i를 예측함.
P, Q : embedding layer matrix, 세타f : interaction function
f : multi-layer neural network로 정의하여 오른쪽 항과 같은 식이 성립함.
Training (Learning NCF)
NCF는 0과 1사이의 예측값을 갖고, 데이터는 이진 데이터로 이뤄져 있음.
likelihood function - Bernoulli dstn :
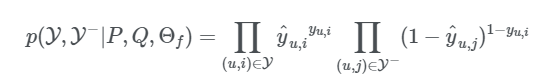
loss function을 최소화하는 objective function으로 parameter 찾기

GMF (Generalized Matrix Factorization)

MF는 NCF의 특별한 케이스가 됨을 보여줌. → GMF
yu,i를 아래와 같이 파라미터라이징을 하면 이는 MF가 됨.
h를 [1, 1, 1, .. , 1] 형태의 uniform vector, a_out을 identity function, ⊙를 element-wise product로 가정하면 NCF framework는 Matrix Factorization과 동일해짐.
논문에서는 a_out=σ(x)=1/(1+e−x)로 지정하고, h를 학습 가능한 non-uniform weight로 지정하여 latent feature 사이의 중요도를 고려할 수 있도록 하였음.
MLP (Multi-Layer Perceptron)
MLP도 NCF의 특별한 케이스가 됨을 보여줌.
GMF는 linear하고 fixed한 특징 때문에 user와 item 간의 복잡한 관계를 표현하지 못하는 반면 MLP는 non-linear하고 flexible하기 때문에 복잡한 관계를 표현할 수 있음.

ϕ1은 user와 item의 latent vector를 concatenation하는 함수임.
ϕl(l≥2)은 Neural Net 함수로 W와 b는 각각 가중치 행렬과 편향 벡터를 나타냄. 마지막 식은 GMF의 구조와 동일하나 차이점은 GMF는 ϕ1(.)가 linear구조인 반면, MLP는 ϕL(.)가 non-linear 구조여서 복잡한 관계를 학습할 수 있음.
Fusion of GMF and MLP
GMF와 MLP를 통합한 모델 제시 ( → neural matrix factorization )
서로 다른 embedding layer를 사용한다는 것임.
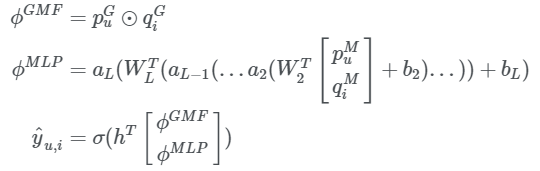
여기서 (pG, qG) (pM, qM)은 각각 GMF와 MLP의 embedding matrix임.
→ 서로 다른 embedding layer를 사용한다는 의미는 두 벡터의 차원이 다를 수 있다는 것.
최종 값은 각 모델에서 나온 GMF와 MLP의 output을 concatenation하여 ℎ로 가중치를 줘 최종 추정치를 구하게 됨.
→ user-item간의 상호 작용을 표현하기 위해 MF의 linearity 와 MLP의 non-linearity를 확인할 수 있음.



